Crack Detection Matlab Code For Convolution

1. Linear Convolution In Matlab
2. Convolution Program In Matlab
3. Convolution Matlab Code
4. Matlab Convolution Function

Overview

A blog for beginners. MATLAB image processing codes with examples, explanations and flow charts. MATLAB GUI codes are included. Audio tester crack. I used the following code:%CONVOLUTION IN MATLAB with conv2 clear%INPUT MATRIX. Conversion Edge detection Photoshop effects in MATLAB MATLAB BUILTIN FUNCTIONS Morphological Image Processing Video. Get the code from here: In this. I intend to peform Laplacian of Gaussian edge operator in matlab. This is the knowledge i have LOG operators are second-order deriatives operator. Second order deriatives operator result in zero.

The first step for edge detection using Octave is to convert the image to gray scale. It can be achieved with the following lines of code: // Figure (2): Lena ' s picture in gray scale pkg load image; imggray = rgb2gray(img); figure (2), imshow (imggray).

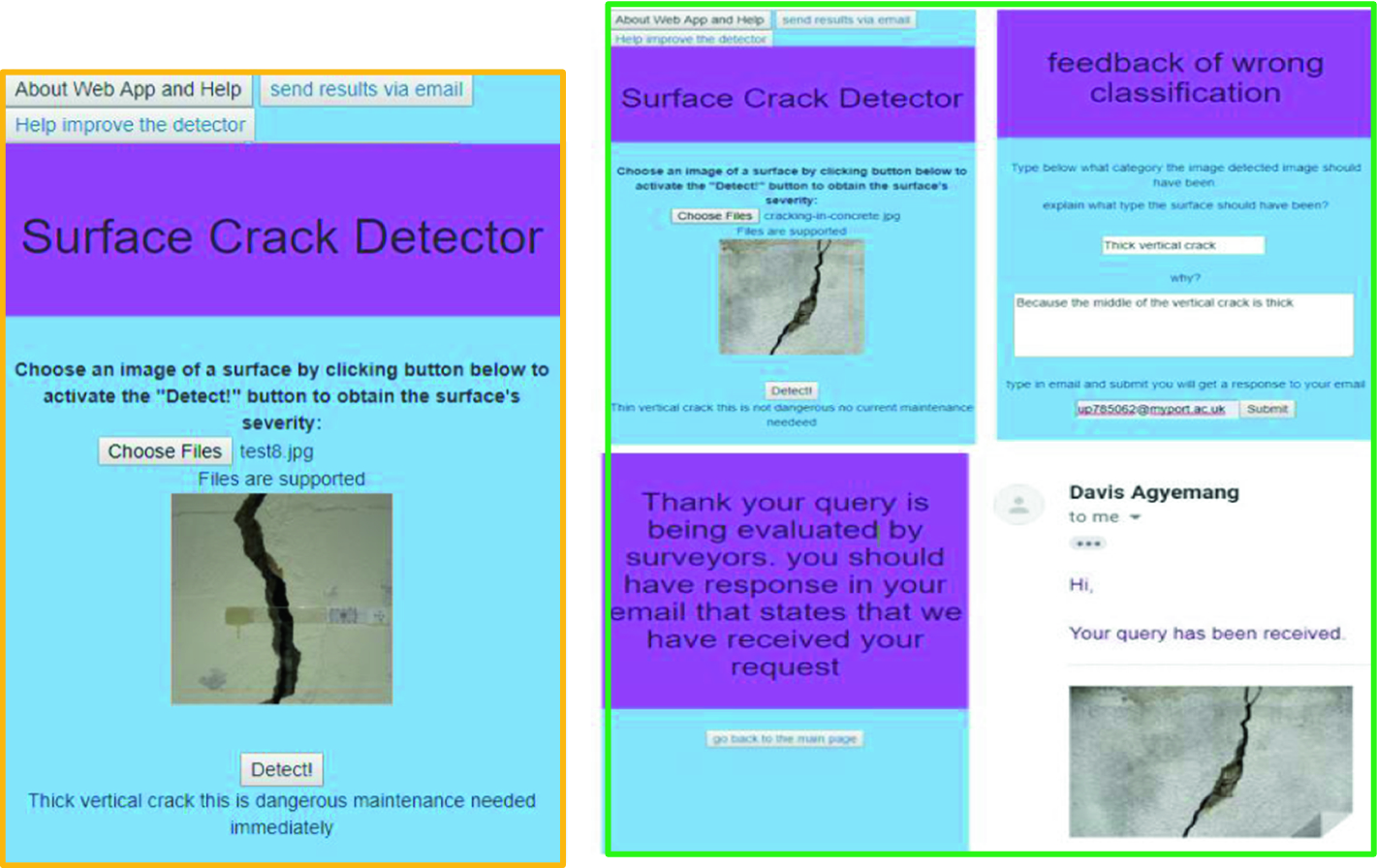
In this exercise you will implement a convolutional neural network for digit classification. The architecture of the network will be a convolution and subsampling layer followed by a densely connected output layer which will feed into the softmax regression and cross entropy objective. You will use mean pooling for the subsampling layer. You will use the back-propagation algorithm to calculate the gradient with respect to the parameters of the model. Finally you will train the parameters of the network with stochastic gradient descent and momentum.

We have provided some MATLAB starter code. You should write your code at the places indicated in the files 'YOUR CODE HERE'. You have to complete the following files: cnnCost.m, minFuncSGD.m. The starter code in cnnTrain.m shows how these functions are used.

Dependencies

We strongly suggest that you complete the convolution and pooling, multilayer supervised neural network and softmax regression exercises prior to starting this one.

Step 0: Initialize Parameters and Load Data

In this step we initialize the parameters of the convolutional neural network. You will be using 10 filters of dimension 9x9, and a non-overlapping, contiguous 2x2 pooling region.

We also load the MNIST training data here as well.

Step 1: Implement CNN Objective

Implement the CNN cost and gradient computation in this step. Your network will have two layers. The first layer is a convolutional layer followed by mean pooling and the second layer is a densely connected layer into softmax regression. The cost of the network will be the standard cross entropy between the predicted probability distribution over 10 digit classes for each image and the ground truth distribution.

Step 1a: Forward Propagation

Convolve every image with every filter, then mean pool the responses. This should be similar to the implementation from the convolution and pooling exercise using MATLAB's conv2 function. You will need to store the activations after the convolution but before the pooling for efficient back propagation later.

Following the convolutional layer, we unroll the subsampled filter responses into a 2D matrix with each column representing an image. Using the activationsPooled matrix, implement a standard softmax layer following the style of the softmax regression exercise.

Step 1b: Calculate Cost

Generate the ground truth distribution using MATLAB's sparse function from the labels given for each image. Using the ground truth distribution, calculate the cross entropy cost between that and the predicted distribution.

Note at the end of this section we have also provided code to return early after computing predictions from the probability vectors computed above. This will be useful at test time when we wish make predictions on each image without doing a full back propagation of the network which can be rather costly.

Step 1c: Back Propagation

First compute the error, delta_d, from the cross entropy cost function w.r.t. the parameters in the densely connected layer. You will then need to propagate this error through the subsampling and convolutional layer. Use MATLAB's kron function to upsample the error and propagate through the pooling layer.

To propagate error through the convolutional layer, you simply need to multiply the incoming error by the derivative of the activation function as in the usual back propagation algorithm. Using these errors to compute the gradient w.r.t to each weight is a bit trickier since we have tied weights and thus many errors contribute to the gradient w.r.t. a single weight. We will discuss this in the next section.

Step 1d: Gradient Calculation

Compute the gradient for the densely connected weights and bias, W_d and b_d following the equations presented in multilayer neural networks.

In order to compute the gradient with respect to each of the filters for a single training example (i.e. image) in the convolutional layer, you must first convolve the error term for that image-filter pair as computed in the previous step with the original training image. Again, use MATLAB's conv2 function with the ‘valid' option to handle borders correctly. Make sure to flip the error matrix for that image-filter pair prior to the convolution as discussed in the simple convolution exercise. The final gradient for a given filter is the sum over the convolution of all images with the error for that image-filter pair.

The gradient w.r.t to the bias term for each filter in the convolutional layer is simply the sum of all error terms corresponding to the given filter.

Make sure to scale your gradients by the inverse size of the training set if you included this scale in the cost calculation otherwise your code will not pass the numerical gradient check.

Step 2: Gradient Check

Use the computeNumericalGradient function to check the cost and gradient of your convolutional network. We've provided a small sample set and toy network to run the numerical gradient check on.

Once your code passes the gradient check you're ready to move onto training a real network on the full dataset. Make sure to switch the DEBUG boolean to false in order not to run the gradient check again.

Linear Convolution In Matlab

Step 3: Learn Parameters

Using a batch method such as L-BFGS to train a convolutional network of this size even on MNIST, a relatively small dataset, can be computationally slow. A single iteration of calculating the cost and gradient for the full training set can take several minutes or more. Thus you will use stochastic gradient descent (SGD) to learn the parameters of the network.

You will use SGD with momentum as described in Stochastic Gradient Descent. Implement the velocity vector and parameter vector update in minFuncSGD.m.

In this implementation of SGD we use a relatively heuristic method of annealing the learning rate for better convergence as learning slows down. We simply halve the learning rate after each epoch. As mentioned in Stochastic Gradient Descent, we also randomly shuffle the data before each epoch, which tends to provide better convergence.

Step 4: Test

With the convolutional network and SGD optimizer in hand, you are now ready to test the performance of the model. We've provided code at the end of cnnTrain.m to test the accuracy of your networks predictions on the MNIST test set.

Run the full function cnnTrain.m which will learn the parameters of you convolutional neural network over 3 epochs of the data. This shouldn't take more than 20 minutes. After 3 epochs, your networks accuracy on the MNIST test set should be above 96%.

Congratulations, you've successfully implemented a Convolutional Neural Network! Voice effects for discord mac.

Applet: Katie Dektar
Text: Marc Levoy
Technical assistance: Andrew Adams

Convolution is an operation on two functions f and g, which produces a third function that can be interpreted as a modified ('filtered') version of f. In this interpretation we call g the filter. If f is defined on a spatial variable like x rather than a time variable like t, we call the operation spatial convolution. Convolution lies at the heart of any physical device or computational procedure that performs smoothing or sharpening. Applied to two dimensional functions like images, it's also useful for edge finding, feature detection, motion detection, image matching, and countless other tasks. Formally, for functions f(x) and g(x) of a continuous variable x, convolution is defined as:
where * means convolution and · means ordinary multiplication. For functions of a discrete variable x, i.e. arrays of numbers, the definition is:
Finally, for functions of two variables x and y (for example images), these definitions become:
and
In digital photography, the image produced by the lens is a continuous function f(x,y), Placing an antialiasing filter in front of the sensor convolves this image by a smoothing filter g(x,y). This is the third equation above. Once the image has been recorded by a sensor and stored in a file, loading the file into Photoshop and sharpening it using a filter g[x,y] is the fourth equation.

Despite its simple definition, convolution is a difficult concept to gain an intuition for, and the effect obtained by applying a particular filter to a particular function is not always obvious. In this applet, we explore convolution of continuous 1D functions (first equation) and discrete 2D functions (fourth equation).

Convolution of 1D functions

On the left side of the applet is a 1D function ('signal'). This is f. You can draw on the function to change it, but leave it alone for now. Beneath this is a menu of 1D filters. This is g. If you select 'custom' you can also draw on the filter function, but leave that game for later. At the bottom is the result of convolving f by g. Click on a few of the filters. Notice that 'big rect' blurs f more than 'rect', but it leaves kinks here and there. Notice also that 'gaussian' blurs less than 'big rect' but doesn't leave kinks.

Both functions (f and g) are drawn as if they were functions of a continuous variable x, so it would appear that this visualization is showing convolution of continuous functions (first equation above). In practice the two functions are sampled finely and represented using 1D arrays. These numbers are connected using lines when they are drawn, giving the appearance of continuous functions. The convolution actually being performed in the applet's script is of two discrete functions (second equation above).

Whether we treat the convolution as continuous or discrete, its interpretation is the same: for each position x in the output function, we shift the filter function g left or right until it is centered at that position, we flip it left-to-right, we multiply every point on f by the corresponding point on our shifted g, and we add (or integrate) these products together. The left-to-right flipping is because, for obscure reasons, the equation for convolution is defined as g[x-k], not g[x+k] (using the 2nd equation as an example).

An alternative way to think about convolution

If this procedure is a bit hard to wrap your head around, here's an equivalent way to describe it that may be easier to visualize: at each position x in the output function, we place a copy of the filter g, centered left-to-right around that position, flipped left-to-right, and scaled up or down according to the value of the signal f at that position. After laying down these copies, if we add them all together at each x, we get the right answer!

To see this alternative way of understanding convolution in action, click on 'animate', then 'big rect'. The animation starts with the original signal f, then places copies of the filter g at positions along f, stretching them vertically according to the height of f at that position, then adds these copies together to make the thick output curve. Although the animation only shows a couple dozen copies of the filter, in reality there would need to be one copy for every position x. In addition, for this procedure to work the sum of copies must be divided by the area under the filter function, a processing called normalization. Otherwise, the output would be higher or lower than the input, rather than simply being smoothed or sharpened. For all the filters except 'custom', normalization is performed for you just before drawing the thick output curve. For the 'custom' filter, see below.

Convolution Program In Matlab

Once you understand how this works, try the 'sharpen' or 'shift' filters. The sharpen filter replaces each value of f with a weighted sum of its immediate neighbors, but subtracting off the values of neighbors a bit further away. The effect of these subtractions is to exaggerate features in the original signal. The 'Sharpen' filter in Photoshop does this; so do certain layers of neurons in your retina. The shift filter replaces each value of f with a value of f taken from a neighbor some distance to the right. (Yes, to the right, even though the spike in the filter is on the left side. Remember that convolution flips the filter function left-to-right before applying it.)

Finally, click on 'custom' and try drawing your own filter. If the area under your filter is more or less than 1.0, the output function will jump up or down, respectively. To avoid this, click on 'normalize'. This will scale your filter up or down until its area is exactly 1.0. By the way, if you animate the application of your custom filter, the scaled copies will only touch the corresponding point on the original function if your custom filter reached y=1.0 at its x=0 position. Regardless, if your filter is normalized, the output function will be of the right height.

Convolution Matlab Code

Convolution of 2D functions

On the right side of the applet we extend these ideas to two-dimensional discrete functions, in particular ordinary photographic images. The original 2D signal is at top, the 2D filter is in the middle, depicted as an array of numbers, and the output is at the bottom. Click on the different filter functions and observe the result. The only difference between 'sharpen' and 'edges' is a change of the middle filter value from 9.00 to 8.00. However, this change is crucial, as you can see. In particular, the sum of all non-zero filter values in 'edges' is zero. Therefore, for positions in the original signal that are smooth (like the background), the output of the convolution is zero (i.e. black). The filter 'hand shake' approximates what happens in a long-exposure photograph, in this case if the camera's aim wanders from upper-left to lower-right during the exposure.

Finally, click on 'identity', which sets the middle filter tap (as positions in a filter are sometimes called) to 1.0 and the rest to 0.0. It should come as no surprise that this merely makes a copy of the original signal. Now click on 'custom', then click on individual taps and enter new values for them. As you enter each value, the convolution is recomputed. Try creating a smoothing filter, or a sharpening filtering. Or starting with 'identity', change the middle tap to 0.5, or 2.0. Does the image scale down or up in intensity? The applet is clipping outputs at 0.0 (black) and 255.0 (white), so if you try to scale intensites up, the image will simply saturate - like a camera if your exposure were too long. Try putting 1.0's in the upper-left corner and the lower right corner, setting everything else to 0.0. Do you get a double image? As with the custom 1D filter, if your filter values don't sum to 1.0, you might need to press 'normalize'. Unless you're doing edge finding, in which case they should sum to 0.0.

Matlab Convolution Function

We also load the MNIST training data here as well.

Step 1: Implement CNN Objective

Implement the CNN cost and gradient computation in this step. Your network will have two layers. The first layer is a convolutional layer followed by mean pooling and the second layer is a densely connected layer into softmax regression. The cost of the network will be the standard cross entropy between the predicted probability distribution over 10 digit classes for each image and the ground truth distribution.

Step 1a: Forward Propagation

Convolve every image with every filter, then mean pool the responses. This should be similar to the implementation from the convolution and pooling exercise using MATLAB's conv2 function. You will need to store the activations after the convolution but before the pooling for efficient back propagation later.

Following the convolutional layer, we unroll the subsampled filter responses into a 2D matrix with each column representing an image. Using the activationsPooled matrix, implement a standard softmax layer following the style of the softmax regression exercise.

Step 1b: Calculate Cost

Generate the ground truth distribution using MATLAB's sparse function from the labels given for each image. Using the ground truth distribution, calculate the cross entropy cost between that and the predicted distribution.

Note at the end of this section we have also provided code to return early after computing predictions from the probability vectors computed above. This will be useful at test time when we wish make predictions on each image without doing a full back propagation of the network which can be rather costly.

Step 1c: Back Propagation

First compute the error, delta_d, from the cross entropy cost function w.r.t. the parameters in the densely connected layer. You will then need to propagate this error through the subsampling and convolutional layer. Use MATLAB's kron function to upsample the error and propagate through the pooling layer.

To propagate error through the convolutional layer, you simply need to multiply the incoming error by the derivative of the activation function as in the usual back propagation algorithm. Using these errors to compute the gradient w.r.t to each weight is a bit trickier since we have tied weights and thus many errors contribute to the gradient w.r.t. a single weight. We will discuss this in the next section.

Step 1d: Gradient Calculation

Compute the gradient for the densely connected weights and bias, W_d and b_d following the equations presented in multilayer neural networks.

In order to compute the gradient with respect to each of the filters for a single training example (i.e. image) in the convolutional layer, you must first convolve the error term for that image-filter pair as computed in the previous step with the original training image. Again, use MATLAB's conv2 function with the ‘valid' option to handle borders correctly. Make sure to flip the error matrix for that image-filter pair prior to the convolution as discussed in the simple convolution exercise. The final gradient for a given filter is the sum over the convolution of all images with the error for that image-filter pair.

The gradient w.r.t to the bias term for each filter in the convolutional layer is simply the sum of all error terms corresponding to the given filter.

Make sure to scale your gradients by the inverse size of the training set if you included this scale in the cost calculation otherwise your code will not pass the numerical gradient check.

Step 2: Gradient Check

Use the computeNumericalGradient function to check the cost and gradient of your convolutional network. We've provided a small sample set and toy network to run the numerical gradient check on.

Once your code passes the gradient check you're ready to move onto training a real network on the full dataset. Make sure to switch the DEBUG boolean to false in order not to run the gradient check again.

Linear Convolution In Matlab

Step 3: Learn Parameters

Using a batch method such as L-BFGS to train a convolutional network of this size even on MNIST, a relatively small dataset, can be computationally slow. A single iteration of calculating the cost and gradient for the full training set can take several minutes or more. Thus you will use stochastic gradient descent (SGD) to learn the parameters of the network.

You will use SGD with momentum as described in Stochastic Gradient Descent. Implement the velocity vector and parameter vector update in minFuncSGD.m.

In this implementation of SGD we use a relatively heuristic method of annealing the learning rate for better convergence as learning slows down. We simply halve the learning rate after each epoch. As mentioned in Stochastic Gradient Descent, we also randomly shuffle the data before each epoch, which tends to provide better convergence.

Step 4: Test

With the convolutional network and SGD optimizer in hand, you are now ready to test the performance of the model. We've provided code at the end of cnnTrain.m to test the accuracy of your networks predictions on the MNIST test set.

Run the full function cnnTrain.m which will learn the parameters of you convolutional neural network over 3 epochs of the data. This shouldn't take more than 20 minutes. After 3 epochs, your networks accuracy on the MNIST test set should be above 96%.

Congratulations, you've successfully implemented a Convolutional Neural Network! Voice effects for discord mac.

Applet: Katie Dektar
Text: Marc Levoy
Technical assistance: Andrew Adams

Convolution is an operation on two functions f and g, which produces a third function that can be interpreted as a modified ('filtered') version of f. In this interpretation we call g the filter. If f is defined on a spatial variable like x rather than a time variable like t, we call the operation spatial convolution. Convolution lies at the heart of any physical device or computational procedure that performs smoothing or sharpening. Applied to two dimensional functions like images, it's also useful for edge finding, feature detection, motion detection, image matching, and countless other tasks. Formally, for functions f(x) and g(x) of a continuous variable x, convolution is defined as:
where * means convolution and · means ordinary multiplication. For functions of a discrete variable x, i.e. arrays of numbers, the definition is:
Finally, for functions of two variables x and y (for example images), these definitions become:
and
In digital photography, the image produced by the lens is a continuous function f(x,y), Placing an antialiasing filter in front of the sensor convolves this image by a smoothing filter g(x,y). This is the third equation above. Once the image has been recorded by a sensor and stored in a file, loading the file into Photoshop and sharpening it using a filter g[x,y] is the fourth equation.

Despite its simple definition, convolution is a difficult concept to gain an intuition for, and the effect obtained by applying a particular filter to a particular function is not always obvious. In this applet, we explore convolution of continuous 1D functions (first equation) and discrete 2D functions (fourth equation).

Convolution of 1D functions

On the left side of the applet is a 1D function ('signal'). This is f. You can draw on the function to change it, but leave it alone for now. Beneath this is a menu of 1D filters. This is g. If you select 'custom' you can also draw on the filter function, but leave that game for later. At the bottom is the result of convolving f by g. Click on a few of the filters. Notice that 'big rect' blurs f more than 'rect', but it leaves kinks here and there. Notice also that 'gaussian' blurs less than 'big rect' but doesn't leave kinks.

Both functions (f and g) are drawn as if they were functions of a continuous variable x, so it would appear that this visualization is showing convolution of continuous functions (first equation above). In practice the two functions are sampled finely and represented using 1D arrays. These numbers are connected using lines when they are drawn, giving the appearance of continuous functions. The convolution actually being performed in the applet's script is of two discrete functions (second equation above).

Whether we treat the convolution as continuous or discrete, its interpretation is the same: for each position x in the output function, we shift the filter function g left or right until it is centered at that position, we flip it left-to-right, we multiply every point on f by the corresponding point on our shifted g, and we add (or integrate) these products together. The left-to-right flipping is because, for obscure reasons, the equation for convolution is defined as g[x-k], not g[x+k] (using the 2nd equation as an example).

An alternative way to think about convolution

If this procedure is a bit hard to wrap your head around, here's an equivalent way to describe it that may be easier to visualize: at each position x in the output function, we place a copy of the filter g, centered left-to-right around that position, flipped left-to-right, and scaled up or down according to the value of the signal f at that position. After laying down these copies, if we add them all together at each x, we get the right answer!

To see this alternative way of understanding convolution in action, click on 'animate', then 'big rect'. The animation starts with the original signal f, then places copies of the filter g at positions along f, stretching them vertically according to the height of f at that position, then adds these copies together to make the thick output curve. Although the animation only shows a couple dozen copies of the filter, in reality there would need to be one copy for every position x. In addition, for this procedure to work the sum of copies must be divided by the area under the filter function, a processing called normalization. Otherwise, the output would be higher or lower than the input, rather than simply being smoothed or sharpened. For all the filters except 'custom', normalization is performed for you just before drawing the thick output curve. For the 'custom' filter, see below.

Convolution Program In Matlab

Once you understand how this works, try the 'sharpen' or 'shift' filters. The sharpen filter replaces each value of f with a weighted sum of its immediate neighbors, but subtracting off the values of neighbors a bit further away. The effect of these subtractions is to exaggerate features in the original signal. The 'Sharpen' filter in Photoshop does this; so do certain layers of neurons in your retina. The shift filter replaces each value of f with a value of f taken from a neighbor some distance to the right. (Yes, to the right, even though the spike in the filter is on the left side. Remember that convolution flips the filter function left-to-right before applying it.)

Finally, click on 'custom' and try drawing your own filter. If the area under your filter is more or less than 1.0, the output function will jump up or down, respectively. To avoid this, click on 'normalize'. This will scale your filter up or down until its area is exactly 1.0. By the way, if you animate the application of your custom filter, the scaled copies will only touch the corresponding point on the original function if your custom filter reached y=1.0 at its x=0 position. Regardless, if your filter is normalized, the output function will be of the right height.

Convolution Matlab Code

Convolution of 2D functions

On the right side of the applet we extend these ideas to two-dimensional discrete functions, in particular ordinary photographic images. The original 2D signal is at top, the 2D filter is in the middle, depicted as an array of numbers, and the output is at the bottom. Click on the different filter functions and observe the result. The only difference between 'sharpen' and 'edges' is a change of the middle filter value from 9.00 to 8.00. However, this change is crucial, as you can see. In particular, the sum of all non-zero filter values in 'edges' is zero. Therefore, for positions in the original signal that are smooth (like the background), the output of the convolution is zero (i.e. black). The filter 'hand shake' approximates what happens in a long-exposure photograph, in this case if the camera's aim wanders from upper-left to lower-right during the exposure.

Finally, click on 'identity', which sets the middle filter tap (as positions in a filter are sometimes called) to 1.0 and the rest to 0.0. It should come as no surprise that this merely makes a copy of the original signal. Now click on 'custom', then click on individual taps and enter new values for them. As you enter each value, the convolution is recomputed. Try creating a smoothing filter, or a sharpening filtering. Or starting with 'identity', change the middle tap to 0.5, or 2.0. Does the image scale down or up in intensity? The applet is clipping outputs at 0.0 (black) and 255.0 (white), so if you try to scale intensites up, the image will simply saturate - like a camera if your exposure were too long. Try putting 1.0's in the upper-left corner and the lower right corner, setting everything else to 0.0. Do you get a double image? As with the custom 1D filter, if your filter values don't sum to 1.0, you might need to press 'normalize'. Unless you're doing edge finding, in which case they should sum to 0.0.

Matlab Convolution Function